The compressible Navier-Stokes equations
In computational fluid dynamics (CFD), the Navier-Stokes equations are often solved in an Eulerian, fixed-in-space, frame. Furthermore, it is also convenient to take the fixed frame as being the aeroplane rather than the air, meaning that the object (wing or aeroplane) is at rest and the air is rushing by. The Eulerian form is what I refer to as the compressible Navier-Stokes equations, or just Navier-Stokes equations. The alternative to the Eulerian frame is the so-called Lagrangian, whereby the equations are describing the motion of infinitesimal mass elements of the fluid. These two versions are mathematically equivalent if the velocity field is sufficiently smooth, which is a rather strong assumption. There is also the incompressible Navier-Stokes equations that model, as the name implies, a for all practical purposes incompressible fluid such as water. Since the fluid is incompressible, thermodynamics does not play a role and the speed of sound is «infinite». Mathematically, the equations have a different structure (elliptic-parabolic) than the compressible equations (hyperbolic-parabolic). Here, I do not discuss the incompressible equations, but one should note that the compressible equations should, in some sense, «turn into» the incompressible if the density happens to be constant. The compressible equations are:
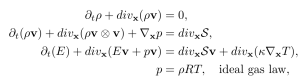
These equations describe the conservation of mass, momentum and energy. rho is the density; v the velocity; p is pressure; S the stress tensor; E the total energy; T temperature; kappa is the heat conductivity coefficient; mu the viscosity coefficient; R is the gas constant.
The hyperbolic continuity equation
Perhaps, the most eye-catching feature of the (compressible) Navier-Stokes equations, is the zero on the right-hand of the continuity (mass) equation. The other equations, conservation of momentum and energy, have diffusive/viscous terms on the right-hand side and the zero breaks this symmetry.
This zero is a real troublemaker. One example has to do with the boundary conditions. For a scalar hyperbolic equation (like the inviscid Burgers equation), an inflow requires one boundary condition and an outflow none. (So-called characteristic boundary condition.) For fully parabolic conservation laws (like the viscous Burger equation), this physically intuitive way of setting boundary conditions is easily generalised. However, the zero in the Navier-Stokes equations destroys this structure in one (subsonic outflow) out of four different flow cases (subsonic in- and outflow and supersonic in- and outflow).
Instead, complicated and rather unintuitive workarounds have to be devised and these do not work well in practice. What does work well, although mathematically incorrect, is to set the physically intuitive boundary conditions as if the system was completely parabolic. In practice, this is what is commonly done.
Another issue that emanate from this zero when attempting to prove well-posedness is positivity, i.e., that density, temperature and pressure remain non-negative. For the Navier-Stokes equations it can not be proven, without strong a priori stability assumptions, that a solution beginning with sensible data will not evolve to a solution that violates positivity. In fact, negative density or pressure is the most common reason for a CFD code to crash which has spawned research into numerical fixes that prevent this. Nevertheless, a model is not designed to be convenient for mathematical and numerical analysts; it is supposed to be good a model, although it cannot be emphasized enough that well-posedness is instrumental for predictive simulations. (Unlike for linear PDEs, it is perfectly possible that a consistent numerical approximation of a non-linear conservation law is stable, in the sense that the solution does not grow beyond bounds, while still being entirely wrong.)
But it is not only from a mathematical/numerical perspective that negative densities are troublesome. It stands to reason that if a compressible flow model is given reasonable initial data, it does not evolve to an unphysical solution. There are in fact a number of physically strange properties of the Navier-Stokes equations, that all emanate from the zero in the continuity equation. Namely, there may be a non-zero entropy and energy gradient through an adiabatic wall; relaxation to thermodynamic equilibrium requires convective transport even at the diffusive scale; remarkably complicated (and physically inexplicable) models are required for multi-component flows in order to not violate the non-diffusive continuity equation of the Navier-Stokes equation.
Predictive numerical simulations
The design of a numerical scheme through numerical analysis usually follows the same pattern: Find a proof of well-posedness in the literature and then design a numerical scheme that converges to the mathematical solution. That means that one mimics the properties of the solution. The problem is that such a theorem is not available for the Navier-Stokes equations. In fact, proving well-posedess is awarded with a rather hefty lump of money. (A huge stumbling block is the zero in the continuity equation.)
So, it is unknown what properties numerical solution should have. This may sound as an academic problem but it means that numerical solutions may, or may not, be approximate solutions to the Navier-Stokes equation. This uncertainty is very much is a practical problem.
Today, useful engineering CFD is often carried out by teams of scientist and engineers. Apart from the numerics and physics, it takes experience and technical skills to produce good computational grids and production CFD codes must run fast on parallel (nowadays often heterogeneous) machines, which calls for the skills of computer scientists. Through validation and testing, a computational tool can then be developed. When running a new problem that is similar to the validation cases, the result can be trusted with a reasonable confidence. However, the more the problem is changed, the less the results can be trusted. Ideally, if a model (the set of equations) has been validated, then any provably convergent code (be it finite difference, discontinuous Galerkin, spectral element or any other method) should produce reliable solutions to any aerodynamic problem as long as it is computationally feasible.
Aerodynamic computations typically require the use of very large grids and are thus very expensive (requires massive computational power) and time consuming. Although, one may need to run a few simulations, with slightly different input, to assess the sensitivity of the problem, it is unfeasible to run it 100s or 1000s of times to obtain statistical data from which a solution is built. The output of a single run has to represent the solution, in some reasonable way (but perhaps not pointwise). For instance, the averaged velocity in some small region of a turbulent flow should accurately represent the mean velocity in that area, although the smallest eddies may be inaccurate. Mathematically, this calls for rather strong notion of well-posedness. Today, such theory seems far away for the Navier-Stokes equations.
Although, there are a number of issues with the Navier-Stokes equations, fact remains that it has been very successful in modelling compressible flows since they are derived from sound physical reasoning. However, it is also a fact that these equations are not fundamental in the same way as other equations in physics. They are not derived exclusively from first principles. It is tempting to speculate that for other, less canonical equations, such huge mathematical difficulties would have prompted scientists to explore other paths.
It should be duly noted that there has been research into modifications of the standard Navier-Stokes equations (e.g. by Brenner), but most often modifications are aimed to improve the physical validity range of the Navier-Stokes equations rather than resolving any well-posedness issues. Somehow, lack of well-posedness is not perceived to be a huge disadvantage of the model. An equally capable, but well-posed model, is consequently not considered to be of much value. Of course, one can also argue that the Navier-Stokes equations have been extensively validated. While this is true, it is generally less true than often assumed by CFD scientists. It is not that computational and experimental data line up on top of each other in all cases. Furthermore, there is a plethora of different models for e.g. viscosity and heat conduction that gives some wiggle room to choose the model best suited for the particular experiment. It would surprising if other compressible flow models derived from similar physical assumptions would not do as well.
Physical foundation of the Navier-Stokes equations
The question, I have asked myself ever since my PhD studies is: Why is there a zero in the continuity equation? It has always puzzled me why mass would not diffuse when diffusion gives rise to momentum (or rather velocity) and temperature diffusion. Many years ago now, I became aware of Brenner’s modification of the Navier-Stokes equations, that introduces mass diffusion and removes the zero in the continuity equation, and that there is a proof that weak solutions exists for this system. (Feireisl&Vasseur, 2010) However, this system was debunked on (in my opinion, erroneous) physical grounds. The Brenner modification is based on the standard Navier-Stokes equations and by introducing separate mass and volume velocities, mass diffusion is introduced into the system. Although, the two velocities can be motivated from physics, it complicates the reasoning in the derivation considerably. What Brenner’s system clearly shows, is that mass diffusion solves many of the mathematical problems of the original system. However, instead of modifying the existing Navier-Stokes system, I went back to the derivation of the Navier-Stokes to see what assumption leads to the zero in the first place.
In textbooks, Navier-Stokes equations are often derived by first deriving the Euler equations. This is, not surprisingly given the name, done in an Eulerian frame. An imaginary box is immersed in the flow, and the flow in and out of it leads to a balance law. To obtain the Navier-Stokes equations, the viscous/diffusive effects must be added to the Euler model. Now, textbooks shift to a Lagrangian frame. That is, the imaginary box now represents a small «mass element» that flows downstream. Being a mass element, it is subject to forces in the flow, which deforms it. This is how, the viscous stress tensor enters the equation. It models the viscous forces acting on the mass element. This view is strikingly similar to structural mechanics and indeed, this was how the equations were derived originally by Stokes.
However, Stokes focused on the derivation of the momentum equation and the continuity equation followed from Newton’s 2nd law and the fact that he considered a mass element. He did not derive the energy equation, which is a later addition to the equations. In the energy equation, the viscous term represent the work done by viscosity. Furthermore, there is a Fourier heat diffusive term, that is typically added to the energy equation in the Eulerian frame.
Countless times have I heard the phrase «mass does not diffuse» as an explanation of the zero in the continuity equation. Given Stokes derivation, one should really say «a Lagrangian mass element can not diffuse mass», but that follows by definition of a mass element. What one also should recognise is that deriving the equations from the dynamics of a mass element is a modelling choice among others.
Returning for a moment to structural mechanics, we note that a mass element makes good sense. In a steel rod, we can «mark» the atoms inside a small box. If we bend the rod slightly the atoms will move, but they will remain in the same internal order. If we let go, the rod returns and all atoms return to their original positions. Atoms in a solid are held in place my electromagnetic forces. Building a continuum theory on mass elements and a stress tensor representing the intermolecular forces, makes perfect sense.
This model of a solid, a collection of molecules arranged in a grid, can also be used to explain heat dissipation. The vibration of molecules is temperature dependent and they will bounce into each other and thereby dissipate temperature through the solid. This process is called conduction and it is perfectly compatible with the mass element view, since all molecules remain in their relative places.
However, a major physical difference between a solid and a gas is that in the latter, the atoms do move. A lot. Arguably, the idea of a mass element does not make sense on the molecular level. Hence, a fluid mass element is not a collection of particles but rather it is a piece of the continuum. That is one has to be careful with what is meant by the «continuum». A continuum variable, such as the pressure, is loosely thought of as a certain local mean value of the cloud of atoms. In fact, one has to be very careful with the meaning of continuum when deriving continuum models, but leaving that aside, we return to the analogy with structural mechanics.
In a fluid the viscous stress tensor arises from the random movements of the atoms. Atoms hit each other and transfer momentum to nearby region, and thereby transferring momentum. However, since gas molecules move relative each other this process is not mainly conductive, but diffusive. This is not contradicting a stress tensor per se. Random movement and collisions of atoms, will give rise to what is perceived as viscosity at the continuum level. An initially sharp interface in the fluid, e.g. between layers of different velocity, will grow fuzzy due to the random transport across the interface. However, if the transfer of momentum of individual molecules across a small distance (on average the mean free path) give rise to a fuzziness of the global momentum, then how come the transfer of mass, by the very same molecules, has no effect at the global scale? Furthermore, the same random movements of molecules give rise to diffusive transport of temperature according to Fourier’s law, which is the only diffusive mechanism acting on the internal energy. However, the internal energy also depends on density and random transport of mass should affect the internal energy as well.
The only way to understand the lack of mass diffusion in the Navier-Stokes equations is if either all collisions occur on the boundary of the mass element such that no molecule crosses, or the same number of molecules pass across the interface in each direction at every moment such that the net transfer is zero. This must be the case, even if the density gradient is large. Physically, that seems very unlikely.
Many common fluids, including air, are modelled as Newtonian fluids. In a Newtonian fluid the viscosity gives rise to a force proportional and perpendicular to velocity gradients. That is, if two sheets of fluid slide against each other, there is a frictional force proportional to the velocity difference between them. In addition, it is assumed that compression or decompression of the mass element diffuse energy. These effects result in the standard stress tensor acting on the mass element in the Lagrangian frame. However, when returning to the Eulerian frame it is very difficult to physically explain some of the terms of the stress tensor. In the Eulerian frame, only forces along the x-axis, should effect the x-momentum, which is not the case unless some additional physical explanation, other the ones mentioned above, is offered.
A new model derived from first principles
In classical mechanics, Newton’s 2nd law is often regarded as a first principle. For a particle, it certainly is, but for a collection of particles, conservation can be viewed as an equally fundamental property.
Instead of flipping to a Lagrangian view, we stick to the Eulerian frame and derive a model by accounting for transport in and out of a fixed-in-space box. As before, the Euler part is readily derived by transport due to velocity. Looking closely at the boundary of the box, we would see molecules travelling randomly across. In doing so, each molecule brings its mass, momentum and energy. All three must thus be diffused at the same rate, which is modelled by simple diffusion terms. In deriving this model, I have only appealed to the conservation principle and the diffusion of particles subject to Brownian motion. (See https://en.wikipedia.org/wiki/Diffusion_equation for a link between Brownian motion and the diffusion equation.) Furthermore, the new model has a much simpler mathematical structure.
nu in the right-hand side is the diffusion coefficient. It takes the value nu=mu/rho.
Today, this model has been validated for a fairly wide range of aerodynamic (and some other) cases, where its solutions have turned out to be indistinguishable from those of the Navier-Stokes equations. In addition, weak solutions, which is a practically useful notion of solutions, have been proven to exist without any a priori assumptions. The proof utilises a convergent numerical scheme meaning that there is a practically usable scheme available that, with mathematical certainty, approximates solutions.
Moreover, the simplicity of the system makes it easier to code and it runs faster. Since it contains diffusive terms in all equations, it relaxes much faster to steady state. Boundary conditions no longer require complicated workarounds. There are no energy or entropy gradients through an adiabatic wall. Multi-component fluids can now be modelled by the generally accepted Fick’s law of diffusion. The equations do not allow density, temperature or pressure to become negative. Diffusion, not convection, relaxes solutions at microscopic scales.
I end this text by pointing to Occam’s razor (https://www.britannica.com/topic/Occams-razor): «Of two competing theories, the simpler explanation of an entity is to be preferred.»