I preface this discussion with a few comments.
- I want the new model to be useful in CFD. Thus, I do not want to make it computationally more complex by adding more equations.
- Hence, the goal is not to extend the range of validity beyond that of the standard Navier-Stokes system.
- The new system models an ideal gas and by that I specifically mean a gas, where the molecules bounce elastically, with no intermolecular forces and with no vibrational and rotational modes that may store energy. The last assumption may be relaxed by including more refined gas laws, heat capacities etc. Modelling intermolecular forces would require additional terms, something that I have not considered so far.
- In classical mechanics, Newton’s 2nd law is often regarded as a first principle. For a particle, it certainly is, but for a collection of particles, conservation can be viewed as an equally fundamental property.
- I use the word diffusion to describe the random motion of molecules.
- I use the word conduction to describe transfer of momentum and kinetic energy due to collisions of molecules.
In summary, the principles used to derive the model are:
- Conservation of mass, momentum and energy in an Eulerian frame.
- Molecular diffusion. At the macroscopic level this modelled by Fourier-type diffusion terms.
- Transfer of macroscopic kinetic energy into macroscopic internal energy by collisions. (Conduction.)
Cloud of molecules to a continuum
To begin with, I consider the 3-D space filled with gas. I divide this space up into small non-overlapping Eulerian (fixed-in-space) boxes that cover the entire domain. The boxes have to be so small that they contain a sufficient number of gas molecules that meaningful averages of mass, velocity, pressure, temperature, etc. may be calculated. (Not PDFs as in kinetic theory, just averages.)
In this way, I obtain a grid of macroscopic variables. To obtain a macroscopic continuum, I then construct a, say twice differentiable, function for each macroscopic variable that interpolates the point values and maintain overall conservation. That is, the integral of the density function equals the total mass of the gas.
Note carefully, that these macroscopic functions represent the gas properties on scales that are sufficiently larger than the microscopic boxes used to define the averages. (I will call them averaging boxes.)
Also, the kinetic energy of the gas cloud is encoded as the total energy at the macroscopic level. The total energy consists of two contributions: 1) the kinetic energy which is computed from the average density and average velocity at a point.;2) the internal energy that accounts for the random-motion part of the molecular kinetic energy.
Non-diffusive continuum model
Next, we use these macroscopic continuum functions to derive flow equations. To this end, we define an Eulerian box in space. This continuum box has to be significantly larger than the averaging boxes, if we are to use the continuum variables to compute in and outflow.
Having defined this box, the Euler equations follow readily from conservation, just like in any textbook on fluid mechanics. For instance, the time rate of change of density is proportional to the momentum in and out flux through the boundaries of the box.
Modelling diffusion
However, this is clearly making an approximation. The boundary of the continuum box is infinitesimally thick in the mathematical derivation and the continuum variables are interpolation functions on finite volumes. Even if the point values used to derive the continuum functions lie exactly on the continuum box boundary, they represent the average of a cloud of molecules, some of which are outside and some are inside the continuum box. If the gas is not perfectly evenly distributed in the averaging box, random motions of the molecules will drive it towards isotropy and thus induce a diffusive transport across the continuum box boundary. Furthermore, when a molecule crosses the continuum box boundary it brings with it its mass, momentum and energy.
At the macroscopic level, diffusive transport of some property is modelled by Fourier/Fick-type diffusion terms. (See https://en.wikipedia.org/wiki/Diffusion_equation for a link between Brownian motion and the diffusion equation.)
Applying the Brownian diffusion model to our observation that gas molecules possess mass, momentum and kinetic energy, we conclude that mass, momentum and total energy must diffuse in the macroscopic model. Furthermore, the diffusion coefficients have to be the same for all three properties since the diffusion coefficient represents the rate at which a property is diffused. Here, the net number of molecules per time unit that passes the continuum box boundary. Since the rate is the same, irrespective if the molecules’ mass, momentum or energy is monitored, the macroscopic diffusion has to be the same.
This leads to the first terms on the right-hand side of the equation below, with diffusion coefficient nu.
Relaxation of internal energy.
In the original model, I only accounted for diffusion across the continuum box boundary. (The nu terms.) This diffusion includes diffusion of total energy, and hence the internal energy. I noted that the temperature part of the diffusion of internal energy was not the same as Fourier’s law appearing in the compressible Navier-Stokes equations. However, in the dcE model internal energy is also transported by the mass diffusion. At the time, I did not know if the dcE model and the NSF would result in the same diffusion of internal energy or not.
Furthermore, I argued that a flow model should have «a pure mode of thermodynamic relaxation». That is, that it should be able to relax to steady state without inducing a macroscopic velocity, something that the NSF has to do in order to relax differences in density.
Generally speaking, determining thermodynamic properties and associated constants is intrinsically difficult in a fluid. For instance, a temperature gradient will induce a gradient in pressure and/or density and eventually induce a non-zero velocity. There is no way around the fact that the model has to be solved for the exact experimental setup in order to determine its constants. Regardless how accurate the measurements are, the model itself can typically never be solved exactly, which in itself may be a considerable source of error.
Nevertheless, evidence suggested that internal energy was not diffused at the correct rate. Hence, I had to understand what diffusive mechanism the original model was missing. The answer (according to my current understanding) is connected to the total energy, which consists of kinetic and internal energy. Returning to the continuum box used to derive the dcE model, one realises that even if there is no diffusion across its interface, collisions within the volume may transfer the «orderly» kinetic energy to the «disorderly» internal energy without changing the total energy. (Recall that the diffusion across the interface does not distinguish between kinetic and internal energy. It models that transport of kinetic energy at the molecular level, which on the macroscopic level is represented by the total energy.)
To model the transfer of energy between the two modes of macroscopic energy, an additional heat diffusive term has to be added to the total energy equation. The only entropy consistent way to do this, is to add a Fourier-type term acting on temperature. (The kappa_T term in the equations below.)
Since there is always an interaction between kinetic and internal energy, pure thermodynamic relaxation is not possible. (Nevertheless, the induced velocity in the dcE model is much smaller than the Navier-Stokes model since it does not have to also effectuate the random mass transport.)
The new model
The current incarnation of the diffusive compressible Euler model, takes the form:
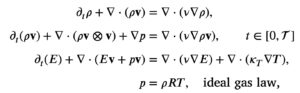
nu in the right-hand side is the diffusion coefficient and kappa_T is a temperature diffusion coefficient.
In comparison with the standard Navier-Stokes moel, the dcE model has a much simpler mathematical structure and its fluxes are much cheaper to compute numerically.
The value for the model coefficient nu, must to leading order be nu=mu/rho. This ensures that Blasius boundary layers are recovered. It is not surprising that its value is related to the viscosity coefficient since both model the effect of random motions in a gas. However, I stress that nu is not a viscosity coefficient. The dcE model does not contain any constitutive law for viscosity.
Furthermore, kappa_T is not the same as kappa appearing in the Navier-Stokes equations. The nu*nabla E term consists heat diffusion and the kappa_T accounts for the discrepancy between that term and the kappa-term in the Navier-Stokes equations.
Today, this model has been validated for a wide range of aerodynamic (and some other) cases, where its solutions have turned out to be indistinguishable from those of the Navier-Stokes equations. In addition, weak solutions, which is a practically useful notion of solutions, have been proven to exist without any a priori assumptions. The proof utilises a convergent numerical scheme meaning that there is a practically usable scheme available that, with mathematical certainty, approximates solutions.
As already mentioned, the simplicity of the system makes it easier to code and it runs faster. Since it contains diffusive terms in all equations, it relaxes much faster to steady state. Boundary conditions no longer require complicated workarounds. There are no energy or entropy gradients through an adiabatic wall. Multi-component fluids can now be modelled by the generally accepted Fick’s law of diffusion. The equations do not allow density, temperature or pressure to become negative. Diffusion, not convection, relaxes solutions at microscopic scales.
I end this text by pointing to Occam’s razor (https://www.britannica.com/topic/Occams-razor): «Of two competing theories, the simpler explanation of an entity is to be preferred.»